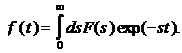1.1.2 Laplace DLTS and beyond  ... an overview

 

L. Dobaczewski and A. R. Peaker

Institute of Physics, Polish Academy of Sciences and Centre for Electronic Materials, Devices and Nanostructures, The University of Manchester

 

Thermal emission of current carriers from defects in semiconductors has been used as a characterisation technique for over fifty years, but perhaps the most significant early publication was by C.T. Sah (Solid State Electronics, 13, 759 (1970)) in which he reviewed his own and earlier work on a quantitative basis. He described many techniques but drew attention to the difficulty of separating emission from closely spaced states and the problems in extracting time constants of exponential decays. In 1974, D.V. Lang (J Appl Phys, 45, 3025 (1974)) introduced a simple form of signal processing to display the temperature dependent emission transients, so producing a sequence of peaks, each of which could be interpreted as relating to an electrically active defect. This technique was named "Deep Level Transient Spectroscopy" (DLTS). Again, in this paper, Lang drew attention to the problem of separating closely spaced transients. Indeed, it has been repeatedly identified as the major deficiency of the technique. DLTS is unlike optical spectroscopy which when conducted at low temperatures can provide very sharp lines. DLTS always produces broad, featureless spectra that are difficult to interpret in terms of precise energetic relationships.

 

Essentially, the time constant resolution of standard DLTS is too poor for studying fine structure in the emission process. Among numerous reasons for this is the fundamental way the spectrum is obtained, i.e., even a perfect defect, with no complicating factors, produces a broad line on the DLTS spectrum. Any variation of time constant present in the defect emission results in an additional broadening of the peak, so this structure is practically impossible to resolve unless the time constants are well separated. Numerous authors have tried to overcome this limitation, usually by applying sophisticated peak de-convolution methods; however, the problem of extracting multiple closely spaced decaying exponentially is fundamentally ill posed.

 

This task of separating multiple, closely spaced, decaying exponential components in measured data recurs throughout science. In DLTS there have been two broad categories of approach which can be classed (perhaps somewhat simplistically) as analogue and digital signal processing. All analogue signal processing is undertaken in real time as the sample temperature is ramped, picking out only one or two decay components at a time. Fixed filters produce an output proportional to the amount of signal that they see within a particular time constant range. This is done by multiplying the capacitance meter output signal by a time-dependent weighting function. Many weighting function wave forms have been. investigated, e.g., double boxcar, [D.V. Lang, J. Appl. Phys. 45, 3023 (1974)], exponential, [J. A. Borsuck and R. M. Swanson, IEEETrans. Electron Devices ED-27, 2217 (1980)], and multiple boxcar, [C.R. Crowell and S. Aliphani, Solid-State Electron 24, 25 (1981)]. In summary, it appears that the most elaborate weighting function wave forms are unable to provide a very significant selectivity improvement over Lang's original scheme.

 

Digital schemes digitise the analogue transient output of the capacitance meter, typically with a sample held at a fixed temperature and averaging many digitised transients to reduce the noise level. All of the accessible decay time constants are then picked out of the acquired wave form by software. The problem of what algorithm to use is difficult. However, consideration in the DLTS specific context is given by lkossi-Anastasiou and Roenker, [K.lkossi-Anastasiou and K. P. Roenker, J Appl. Phys.61, 182 (1987)], who use a "method of moments" approach, and by Nolte and Haller, [D. D. Nolte and E. E. Haller, J. Appl. Phys. 62, 900 (1987)], who used an approximation to the inverse Laplace transform. Nolte and Haller also consider the ultimate theoretical limit of time constant separation in the presence of noise. Eiche et al, [C. Eiche, D. Maier, M.Schneider, D. Sinerius, J. Weese, K. W. Benz, and J. Honerkamp, J. Phys.Condens. Matter 4, 6131 (1992)], use a method "Tikhonov regularisation" to separate the constituent exponentials in a photo-induced current transient spectroscopy (PICTS) signal. Tikhonov regularisation appears to produce results similar to those that we report. More recently a simple scheme using a binomial expansion of the boxcar weighting function was reported by Thurzo, Pogany, and Gmucova, [I. Thurzo, D. Pogany, and K. Gmucova, Solid-State Electron. 35, 1737 (1992)]. This combined a temperature scanning measurement with simple digital signal processing to obtain sharper peaks although this resulted in considerably more noise. A common approach to the quantitative description of non-exponentiality observed in the capacitance transients is to assume that they are characterised by a spectrum of emission rates,

 

 

 where f(t) is the recorded transient and F(s) is the spectral density function. For simplicity, this spectrum is sometimes represented by a Gaussian distribution overlaying the logarithmic emission rate scale, [P.Omling, L. Samuelson, and H. G. Grimmeiss, J. Appl. Phys. 54, 5117 (1983)]. In this way it was possible to describe the non-exponentiality of the transient in terms of broadening of the activation energy for emission. The possibility that the spectrum contains fine structure is ignored.

 

A mathematical representation of the capacitance transients given by the equation is the Laplace transform of the true spectral function F(s). Thus, to find a real spectrum of the emission rates present in the transient it is necessary to use a mathematical algorithm that effectively performs an inverse Laplace transform for the function f(t). The result of such a procedure is a spectrum of delta-like peaks for multi-, mono-exponential transients or a broad spectrum with no fine structure for continuous distribution. In this method it is not necessary to make any a priori assumptions about the functional shape of the spectrum, except that all decays are exponential in the same direction.

 

Despite the fact that we define the problem in a very general way, one has to remember that Eq.(1) has not a general solution for any given function f(t). For an analytical multi-exponential function such a solution exists and, according to Lerch's theorem, [G.A. Korn and T. M.Korn, in Mathematical Handbook (McGraw-Hill, New York, 1968)], it is unique; however, if this function is superimposed with noise the number of possible solutions can be infinite. As a result, our problem is to find the best estimate for F(s) and, according to the prior knowledge about the system being investigated, exclude unphysical solutions and choose only the simplest one, i.e., the one that reveals the least amount of detail or information that was not already known or expected. Following such a strategy one knows that the amount of information obtained from a fitting procedure is as much as necessary to satisfy statistical tests performed on the experimental data. The quantitative improvement in the DLTS measurement resolution which results from the use of this method is presented. The actual algorithm employed is more involved than a simple Laplace transformation; [eg S.W. Provencher, Comp. Phys. Commun. 27, 213 (1982); 27, 229 (1982),]. Indeed one of the principal tasks of the Copernicus Project described here is to explore the application of advanced regularisation techniques to this problem. However, we feel that the end product of a time constant versus spectral density plot justifies our describing this as Laplace DLTS (just as a spectral density-frequency plot is described as a Fourier plot). Different problems related to the Laplace transform inversion and its applicability to the DLTS measurements have been discussed by A. A. Istratov and O. F. Vyvenko in Rev. Sci. Instr., 70, 1233, (1999).

 

Besides a variety of tests performed on the software used for solving Eq.(1), a further test of the method has been undertaken through a long series of measurements on different point and extended defects in different semiconductors. We have investigated the Laplace DLTS spectra starting from a simple point defect in an elemental semiconductor (the platinum-related centre in silicon). In the diagram we show a comparison between a conventional DLTS (a) and Laplace (b) We have also applied the technique to very complicated centres, such as the DX defects in AlGaAs, [L.Dobaczewski, P. Kaczor, M. Missous, A. R. Peaker, and Z. R. Zytkiewicz, Phys. Rev. Lett., 68, 2508 (1992)], GaSb, [L. Dobaczewski, I. D. Hawkins, P. Kaczor, M. Missous, I. Poole, and A.R. Peaker, in Defects in Semiconductors 16, Materials Science Forum, Vols. 83-87, edited by G. Davies, G.G.DeLeo, and M. Stavola (Trans Tech. Zurich, 1991), p. 769], GaAsP, and heavily doped GaAs, [L. Dobaczewski, P. Kaczor, M. Missous, A. R. Peaker, and Z. R. Zytkiewicz J. Appl. Phys. (1995)]. The most important observation from this work is the same in each of the cases but we illustrate the results with AlGaAs:Te. The standard DLTS (c) gave featureless peaks while the Laplace DLTS spectra revealed there is a fine structure in the thermal emission process (d), i.e., each of the defects has its characteristic signature. For the most recent list of publications presenting results obtained with this technique one can find on the web page: http://www.laplacedlts.eu.

 

The evolution of this technique over the last few years has enabled us, by using an isothermal method, to achieve the theoretical limit of resolution of DLTS. For relatively shallow states that emit at low temperature, the reduction in line-width is remarkable and can give us more than two orders of magnitude increase in resolution over Lang's technique. We have devoted much effort to making the technique useable, i.e., establishing stability of the algorithm and improving the hardware so that the theoretical limit is achievable. This is been done under a COPERNICUS contract.